Proyecto 1 en Dibujo Técnico 1ºBTO: creación de un refugio plegable.

Concurso de estructuras organizado por el Instituto de Arquitectura de Shanhái. Equipos procedentes de universidades e institutos de secundaria.

https://ilvwp.com/impresionantes-estructuras-de-carton-echas-por-estudiantes/

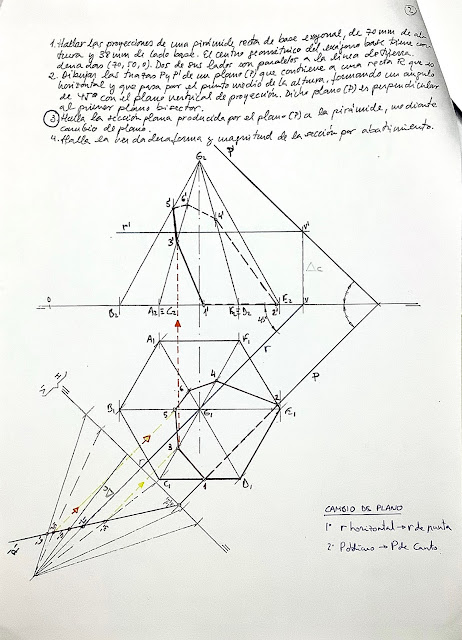
Iniciamos la nueva aventura 2023- 2024 y ya ha habido otro gran desastre natural. Nuestros vecinos marroquíes han sufrido un terremoto devastador y mucha gente se ha quedado sin casa para dormir y guarecerse. Pero por desgracia hay muchísima más gente a nivel mundial que está en su misma situación, tanto por otros desastres naturales como por ser refugiado por una guerra o persecución política. Familias enteras.

Y hay muchos arquitectos e ingenieros sensibles con el tema que buscan soluciones eficaces que abaraten costes y permitan una respuesta rápida.

Y una de las soluciones ha sido la utilización construcciones modulares y/o la técnica del plegado para construir dichos refugios. Empleando el pliegue miura-ori.

Patrón del ejemplo de la derecha. Mediante el plegado pasamos de 2 a 3 dimensiones.

• Pero este tipo de soluciones se usan es más ramas de la ingeniería. Mira este vídeo.
  
  
• Investigadores del Instituto de Tecnología de Georgia, la Universidad de Illinois y la Universidad de Tokio han creado una nueva configuración de soporte estructural inspirada en el origami llamada «tubos de cremallera», consistente en una serie de tubos largos con pliegues en zigzag. Por una parte, los tubos son flexibles y pueden doblarse en una forma de «U». Pero cuando se unen, la estructura que se forma puede ser cien veces más resistente que el material original utilizado para fabricar los tubos.

 Blog sobre innovación en la construcción.

Metodología para el diseño de domos desplegables.

• El plegado también se usa en Diseño y otras disciplinas artísticas.

                             Obras pertenecientes a la serie “Plegar el Vacío” de Pilar Barrios.

  origami-miura-ori-la-ingenieria-papel-pilar-barrios

-------- NUESTRO PROYECTO----------

• En clase bajos a hacer equipos para crear prototipos de refugios. 
• Utilizaremos redes poligonales y un material sostenible como el cartón para construir.

FASES DEL PROYECTO

1. Prácticas guiadas de plegado con patrones suministrados por la profesora.  

2. Creación individual de un patrón miura-ori en cartulina A3.

3. Creación de un prototipo final a escala "infantil" hecho con cartón reciclado. 

Para ello primero se harán prototipos en cartulina a menor tamaño. Y tendrán que hacerse pequeñas pruebas con el material para determinar qué tipo de cartón se necesita en cada caso.

Posiblemente necesitaremos accesorios para realizar alguna unión. Enlace. 

 

Hay más información en esta entrada anterior del blog.

Veamos el resultado del concurso de estructuras organizado por el Instituto de Arquitectura de Shanhái. Equipos procedentes de universidades e institutos de secundaria.

https://ilvwp.com/impresionantes-estructuras-de-carton-echas-por-estudiantes/

Construcción modular con módulos hechos por plegado de cartón. En pequeño se aprecian los prototipos.

Se aprecia que hay uniones hechas con tornillos con rosca, refuerzos-uniones de cartón e incluso cinta adhesiva.

Según el tamaño del prototipo es posible que haya que realizarlo por partes al no haber cartón tan grande.

 

"Ombres lumineuses" Project Team: Katrina Novak, Duc Tran, Pablo Menghini (Toronto)

Sukkahville Design Competition

• Es muy interesante el trabajo que realizan los murcianos CARTONLAB utilizando el cartón como material de construcción y el plegado, diseño modular y con planos seriados. Así que recomiendo bucear en su web. Antigua y nueva. Encontraréis desde diseño de mobiliario a stands y soluciones acústicas. Dejo el enlace a su canal de you tube.
• 
  
   Bee. 

  
  

• Vídeo del Stand de la Feria del vino de Amsterdam.
• Stand de 20m2 realizado íntegramente en cartón Cuádruplex 12,7mm.

Desde su web.

  

 

Plano de3 de los 18 paneles del stand.

https://www.archdaily.pe/pe/724350/stand-ability-diseno-grafico-cartonlab

• Recomiendo adentrase en la obra del japonés Shigeru Ban, el arquitecto del papel, Premio Princesa de la Concordia 2022. Enlace a la reseña de El Confidencial.

http://apuntesdearquitecturadigital.blogspot.com/2019/03/construyendo-con-tubos-de-carton-desde.html

Transformación de un polígono en otro de área equivalente por cortes o cadenas. Las disecciones de Dudeney.

 Así se solucionó un problema de 100 años. Las disecciones de Dudeney.

Problema de aplicación de rectificaciones de Arcos y áreas equivalentes. Hallar el cuadrado equivalente a una circunferencia dada.

Problema de aplicación de rectificaciones de Arcos y áreas equivalentes.

• Hallar el cuadrado equivalente a una circunferencia dada.

Para resolver el problema tendremos que hacer dos partes:

Primera parte.   Rectificar la circunferencia dada.

Pues será el segmento pi•r, de la fórmula de la circunferencia, pi•r cuadrado, el que usemos en la segunda parte del problema.

Segunda parte.    Hallar la cuadratura.

Aplicaremos la fórmula de la media proporcional, según el teorema de la altura de Euclides. 

1. Para ello utilizaremos el segmento hallado en la rectificación, pi•r, como  segmento a   de la fórmula.
2. El segmento b  de la fórmula será el radio de la circunferencia.

El número Áureo. Ejercicios de Dibujo Técnico en Bachillerato. Sección áurea en vídeo.

• Segmento y Rectángulo Áureo.

• Espiral Áurea o de Durero.

• Recomiendo que veáis este documental del programa Redes sobre la proporción áurea.

• ¿Por qué las tarjetas de visita, de crédito o el DNI tienen una dimensión estandarizada? ¿Tienen una proporción especial? Mira el vídeo:
•          Leer este artículo https://lacabezallena.com/diseno/tarjetas/

Sección de una Pirámide recta por plano oblicuo

Materiales para las clases online de DIBUJO TÉCNICO 1ºBTO

PRIMERA CLASE

SISTEMA DIÉDRICO:    repaso del PUNTO

CONTENIDOS para estudiar

• Todo explicado como en nuestra clase:

 1. Cuadrantes, octantes y bisectores.

2. Abatimiento de los  PLANOS DE PROYECCIÓN

3. Proyecciones de un PUNTO.

http://antoniovallecillos.blogspot.com/2015/01/teoria-alfabeto-del-punto-en-sistema.html

4. Coordenadas:      ORIGEN,   ALEJAMIENTO,   COTA

• Online interactivo:   estudiamos con   DIÉDRICO INTERACTIVO de J.A. Cuadrado.

          

     

• Hay que mover el punto (rojo) y ver como cambian los datos que aparecen en la pestañas:                                    Posiciones                  Coordenadas               Notaciones

TAREAS Y LÁMINAS PARA PRACTICAR Y REPASAR  PARA EL EXAMEN DE DIÉDRICO.

• EJERCICIOS INTERACTIVOS

• Dentro de esa aplicación ve a EVALUACIÓN para comprobar si te has enterado.
• Otro cuestionario interactivo con soluciones para comprobar si sabéis ya las posiciones del punto en el espacio

• LÁMINAS
• De las fotocopias que se dieron y/o mandaron anteriormente teníais que tener hechas las láminas: 
• L15 Punto del cuadernillo de vuestro libro.
• PUNTO II   (os he mostrado la solución).  https://drive.google.com/file/d/1ne5VHPOuWBQTxIWpSDVGivQCfjYdjVf5/view
• Tarea nueva:               
1. Lámina PUNTO II (fotocopia).https://drive.google.com/file/d/1ne5VHPOuWBQTxIWpSDVGivQCfjYdjVf5/view
2. Lámina 1 Punto 2007-8. 
3. Lámina 0 Punto 2008-2009
4. Recta: L1 Die I Pto, 
• Tarea nueva:   
1. L2 Die1 Recta, 
2. L3 La Recta 2007-8
3. L16 (ejercicios del cuadernillo de vuestro libro sólo hay que hacer los de rectas). 
• Más complejos por lo que es mejor hacerlos al final:
1. L1 Diédrico . Punto y recta,     
2. L2 Diédrico I.  Recta.
• • Muy bueno es este cuadernillo de láminas de mestreacasa sobre el punto, la recta y el plano. Creo que es  fácil de seguir y no mezcla tipos de ejercicios como en otros.
  • Este es el ENLACE al cuadernillo (se usa en la clase 2):    http://mestreacasa.gva.es/c/document_library/get_filefolderId=500005789339&name=DLFE-946756.pdf
  • No tienen solución hecha por lo que las dudas me las hacéis llegar con una foto comentada a este correo.
  1. Láminas del PUNTO: página 1 y 2..
  
  La nomenclatura no es igual a la nuestra pero creo que sois capaces de usarla.

• Otra OPCIÓN son los ejercicios de PUNTO, RECTA y PLANO de Las Láminas:
• Originales: https://www.laslaminas.es/descargas/diedrico/punto_recta_plano_laminas.pdf
• Soluciones: https://www.laslaminas.es/descargas/diedrico/punto_recta_plano_laminas_solu.pdf

Si alguno no tiene impresora que copie los datos en hojas (más o menos)

INFORMACIÓN EXTRA  de Diédrico sobre la clase de hoy -----------------------------------------

• Presentación animada de Ramón del Águila:
• Alfabeto del punto. Enlace.
•       Representación de puntos por coordenadas.
• Enlace a AG Mírese el vídeo a partir del segundo 10´39´´

Contenidos en vídeo de los canales:

• Universidad Politécnica de Valencia UPV
• AG Dibujo y Mates.
• Juan Escobar.
• Usa letras minúsculas para las trazas y comilla:  v´ y  v, h´ y  h.
• Arturo geometría.
• En estos vídeo aparecen las proyecciones de los puntos escritas de forma diferente a como lo hacemos nosotros. Se usan minúscula y comilla, a´ y a, en lugar de mayúsculas y números, A2 y A1.
• Profesor de Dibujo.
• Cuidado porque en estos vídeos se llama a las trazas de la recta A y B, en lugar de H y V.

VISTAS DIÉDRICAS

• La FLECHA siempre indica el alzado, que es la vista más representativa.

La ubicación de las vistas:

 El alzado siempre está encima de la planta.
 Los perfiles se colocan al revés, es decir, el perfil derecho estará a la izquierda y el izquierdo a la derecha.

Recuerda:

 Misma altura: la pieza es igual de alta en el alzado que en el perfil.

 Mismo ancho: la pieza es igual de ancha el alzado que en la planta.

 Misma profundidad: coincide en la planta y en el perfil.

• A veces hay más de una posibilidad correcta de alzado. Vemos ejemplos de ésto en la web picuino.com  Hay ejercicios en láminas pdf por nivel de dificultad: 

1. Vistas sencillas.
2. Con vistas ocultas. 
3. Con rampas. 
4. Con vistas ocultas y rampas.
5. Con curvas.

Ejercicios simples

Alzado derecho. Formato PDF.

Alzado derecho. Imágenes en formato PNG.

TAREAS DE VISTAS

• Nuevas:
• 1. Las 5 láminas que se pueden descargar, junto con sus soluciones, en la web picuino.com. A ellas pertenecen los ejemplos de arriba.
• Láminas pdf por nivel de dificultad: 
1. Vistas sencillas.
2. Con vistas ocultas. 
3. Con rampas. 
4. Con vistas ocultas y rampas.
5. Con curvas.
• 2. En esta página, gloriamoranmayoespaciodidactico.blogspot.com, también hay enlaces a láminas en pdf con vistas de piezas ordenadas: sencillas, con rampas, con huecos y aristas ocultas, con curvas.
• Hay que hacer las láminas para DIBUJAR LAS VISTAS de una pieza  y LOCALIZAR las PROYECCIONES de los PUNTOS   A  B  C  D  en ELLA. Hay dos niveles:
• 1. Nivel Inicial(2 láminas)

Original y solución en http://gloriamoranmayoespaciodidactico.blogspot.com/2015/10/solidos-ejercicios-de-vistas.html

• 2. Nivel Medio (1 lám). https://drive.google.com/file/d/0B0C-wz68JU6XUy1HNEJZUUVCS0U/view

SEGUNDA  CLASE

SISTEMA DIÉDRICO:    repaso de la Recta.

PERTENENCIAS       

• 1 PUNTO PERTENECE A UNA RECTA  SI --------- LAS PROYECCIONES DEL PUNTO COINCIDEN CON LAS HOMÓNIMAS DE LA RECTA. 

• P2 Pertenece a r2   
• P1 Pertenece a r1   
• P3 pertenece a r3

• Puntos que pertenezcan a rectas.Enlace AG. y  Enlace PdD.

POSICIONES PARTICULARES DE LA RECTA:

• Repaso online interactivo:   estudiamos con   DIÉDRICO INTERACTIVO de J.A. Cuadrado.

          

     

• Hay que mover el punto (rojo) y las trazas para ver como cambian los datos que aparecen en la pestañas:                                    Posiciones      Coordenadas         Notaciones        Tipo

• Vídeo según lo hemos dado en clase:

Se usa nuestra misma forma de nombrar los elementos.

• Para definir una recta necesitamos siempre 2 puntos.
• Pueden ser:
1. 2 puntos cualquiera que pertenezcan a la recta------por lo que las proyecciones del punto coincidirán con las de la recta homónimas.
2. Usar 2 puntos notables llamadas trazas de la recta V y H.
• Son la intersección de la recta con el plano vertical de proyección V y en el plano horizontal de proyección H. En ocasiones se puede usar la traza en el plano de perfil P.
• Se exceptúa la recta de perfil, por ser el único caso en que un punto puede no pertenecer a ella, a pesar de tener sus proyecciones sobre las proyecciones de la recta. Ese punto, por ejemplo, puede tener sus proyecciones P1 y P2 en r1 y r2 pero al ver r3 resulta que P3 no está sobre ella.

• 1. RECTA DEFINIDA POR 2 DE SUS PUNTOS, A y B.

• 2. RECTA DEFINIDA POR SUS TRAZAS  V  H.

1.      Para hallar la traza horizontal Hr1-Hr2, de una recta, se prolonga su proyección vertical r2 hasta su intersección Hr2 con la línea de tierra y por ese punto, se levanta una perpen­dicular a LT hasta su intersección Hr1 con la otra proyección de la recta.
2.      Para hallar la traza vertical Vr1-Vr2 de una rec­ta, se prolonga su proyección horizontal hasta su encuentro en Vr1 con la línea de tierra y por este punto, se levanta una perpendicular a LT hasta su intersección Vr2 con la otra proyección.

     La traza de una recta en el segundo bisector se determina por la intersección de sus dos proyecciones.

1.      Para hallar la traza de una recta con el primer bisector, se halla la simétrica de una de las proyecciones de la recta, respecto a LT, y su intersección con la otra proyección, nos determina una de las proyecciones de la traza.

ALFABETO DE LA RECTA        (TIPOS)

1. Del alfabeto de la recta. Enlace.
2. Recta que pasa-definida por dos puntos de ella.Enlace Art G
3. Representación de la recta de perfil. Enlace UPV.
4. Recta de perfil Enlace youtu.be

• Practica:

• 
  

  EJERCICIOS INTERACTIVOS

  
  
  
  • Cuestionarios interactivos con soluciones para comprobar si sabéis ya:
  • Dentro de esa aplicación ve a EVALUACIÓN para comprobar si te has enterado.
  • Posiciones de la recta.
• 

• HAY RECTAS EN LAS QUE UNA DE LAS PROYECCIONES ESTÁ EN VERDADERA MAGNITUD.

• Practica:

VISIBILIDAD

PARTES VISTAS Y OCULTAS DE UNA RECTA:

1.      Los puntos que separan las partes vistas y ocultas de una recta son, precisamente, sus trazas vistas.
2.      Si las dos trazas son vistas, se ve el segmento determinado por ellas.
3.      Si solamente tiene una traza vista, ésta divide a la recta en dos semirrectas, de las cuales será oculta la que contiene a la traza oculta, y vista la otra.
4.      Si las dos trazas de la recta son ocultas, no se ve ninguna parte de ella.
5.      Para mayor claridad, conviene dibujar con trazo discontinuo las partes ocultas de la recta

Se usa nuestra misma forma de nombrar los elementos.

1. Punto de intersección de una recta con el primer bisector. Enlace UPV.
2. Punto de intersección de una recta común con el 2 bisector. Enlace UPV.

• Practica:

TAREAS DE REPASO PARA EL EXAMEN DE DIÉDRICO

• EJERCICIOS INTERACTIVOS

• Dentro de esa aplicación ve a EVALUACIÓN para comprobar si te has enterado.
• Otro cuestionario interactivo con soluciones para comprobar si sabéis ya las posiciones del punto en el espacio

• LÁMINAS
1. Lo no acabado del Punto de la semana anterior. 
• Tarea nueva:   
1. L2 Die1 Recta, 
2. L3 La Recta 2007-8
3. L16 (ejercicios del cuadernillo de vuestro libro sólo hay que hacer los de rectas). 
• • Muy bueno es este cuadernillo de láminas de mestreacasa sobre el punto, la recta y el plano. Creo que es  fácil de seguir y no mezcla tipos de ejercicios como en otros.
  • Este es el ENLACE al cuadernillo (se usa en la clase 2):    http://mestreacasa.gva.es/c/document_library/get_filefolderId=500005789339&name=DLFE-946756.pdf
  • No tienen solución hecha por lo que las dudas me las hacéis llegar con una foto comentada a este correo.
  1. Láminas de la RECTA: página 3 a la 8.
  
  La nomenclatura no es igual a la nuestra pero creo que sois capaces de usarla.

• Más complejos por lo que es mejor hacerlos al final:
1. L1 Diédrico . Punto y recta,     
2. L2 Diédrico I.  Recta.

• Otra OPCIÓN son los ejercicios de PUNTO, RECTA y PLANO de Las Láminas:
• Originales: https://www.laslaminas.es/descargas/diedrico/punto_recta_plano_laminas.pdf
• Soluciones: https://www.laslaminas.es/descargas/diedrico/punto_recta_plano_laminas_solu.pdf

Si alguno no tiene impresora que copie los datos en hojas (más o menos)

VISTAS

IDENTIFICA EL TIPO DE RECTA QUE ES CADA ARISTA

1. Localiza en las vistas las proyecciones de los puntos A B C  D de las siguientes piezas.

Original y solución en http://gloriamoranmayoespaciodidactico.blogspot.com/2015/10/solidos-ejercicios-de-vistas.html

Veamos cómo se ha hecho en el ejercicio 4 de esta lámina.

•  Puntos que están en el 2 octante:

TAREAS DE VISTAS

• 1. En esta página, gloriamoranmayoespaciodidactico.blogspot.com, también hay enlaces a láminas en pdf con vistas de piezas ordenadas: sencillas, con rampas, con huecos y aristas ocultas, con curvas.
• Hay que hacer las láminas para DIBUJAR LAS VISTAS de una pieza  y LOCALIZAR las PROYECCIONES de los PUNTOS   A  B  C  D  en ELLA. Hay dos niveles:
• 1. Nivel Inicial(2 láminas)

Original y solución en http://gloriamoranmayoespaciodidactico.blogspot.com/2015/10/solidos-ejercicios-de-vistas.html

• 2. Nivel Medio (1 lám). https://drive.google.com/file/d/0B0C-wz68JU6XUy1HNEJZUUVCS0U/view
• 2. Las 5 láminas que se pueden descargar, junto con sus soluciones, en la web picuino.com. A ellas pertenecen los ejemplos de arriba.

TERCERA CLASE

CONTENIDOS A ESTUDIAR

• Rectas especiales: 

1. Recta de máxima pendiente.
2. Recta de máxima inclinación.

RECTAS ESPECIALES

• Recta de MÁXIMA PENDIENTE:su proyección horizontal, r, es perpendicular a la traza                                                                     horizontal del plano.

• Recta de MÁXIMA INCLINACIÓN: su proyección vertical, r’, es perpendicular a la traza                                                                     vertical del plano.

RECTAS CONTENIDAS EN LOS BISECTORES

Recta oblicua.

• Presentación animada de Ramón del Águila:

TAREAS DE REPASO PARA EL EXAMEN DE DIÉDRICO.

1. Terminar de hacer:.
1. Láminas:
1. L15 
2. L16 (ejercicios del cuadernillo).
2. Tarea nueva:               
1. Lámina PUNTO II (fotocopia).
2. Lam fotoc. La recta en el sistema diédrico. Obtener las trazas con PV, PH, !bis,2 bis. Indicar cuadrantes. (Está hecha a mano)
3. Lámina 1 2007-8. 
4. Lámina 2
5. Recta: L1 Die I Pto, 
6. L2 Die1 Recta, 
7. L3 La Recta 2007-8
3. L1 Diédrico . Punto y recta,     
4. L2 Diédrico I.  Recta.

• EJERCICIOS INTERACTIVOS
• Dentro de esa aplicación ve a EVALUACIÓN para comprobar si te has enterado.
• Otro cuestionario interactivo con soluciones para comprobar si sabéis ya las posiciones del punto en el espacio.

DUDAS
Láminas mestre:
D1

D3

 

 

D4

D5

D6

     

L1 Punto y recta. Material de ayuda.

D7

D8

































































































CUARTA CLASE

Recta paralela a la línea de tierra:

     Al ser paralela a LT lo es también a los planos de proyección, por lo tanto carece de trazas, sus dos proyecciones horizontal y vertical son paralelas a LT y están en verdadera magnitud.

3http://sd.joseantoniocuadrado.com/recta.htm

Recta hori­zontal:

     Es una recta paralela al plano horizontal de proyección, por lo cual sólo tiene traza vertical, la proyección horizontal de la recta estará en verdadera magnitud y su proyección vertical será paralela a LT.

Recta frontal:

•      Es una recta paralela al plano vertical de proyección, por lo cual sólo tiene traza horizontal, la proyección vertical de la recta estará en verdadera magnitud y su proyección horizontal será paralela a LT.

Recta de punta:

6. Es un caso particular de la recta horizontal, además de ser paralela al plano horizontal es perpendicular al vertical, su proyección horizontal está en verdadera magnitud y es perpendicular a LT y su proyección vertical es un punto, coincidente con su única traza.

Recta vertical:

Es un caso particular de la recta frontal, además de ser paralela al plano vertical es perpendicular al horizontal, su proyección vertical está en verdadera magnitud y es perpendicular a LT y su proyección horizontal es un punto, coincidente con su única traza.

Recta oblicua:

•      Es una recta oblicua con respecto a los dos planos de proyección, tiene dos trazas y ninguna de sus proyecciones está en verdadera magnitud.

8

Recta que corta a la línea de tierra:

    

• Es una recta oblicua que tiene sus dos trazas confundidas en el mismo punto sobre la línea de tierra.

Recta de perfil:

10

• Es una recta contenida en un plano de perfil, es decir, perpendicular a los dos de proyección, sus dos proyecciones son perpendiculares a LT y necesitaremos auxiliarnos de un plano de perfil para comprobar su inclinación y si un punto pertenece o no a él.

Rectas oblicuas situadas en el 11, 21, 31 y 41 cuadrante:

     Sus características ya se han descrito. En estos ejemplos vemos con claridad la diferencia entre partes vistas y ocultas de una recta.

Recta oblicua contenida en el primer bisector:

•      Será una recta que corte a LT pasando del primer al tercer cuadrante y tenga sus dos proyecciones formando el mismo ángulo con ella.

Recta oblicua contenida en el segundo bisector:

•      Será una recta que corte a LT pasando del segundo al cuarto cuadrante y tenga sus dos proyecciones ocultas y confundidas en la misma recta.

Rectas de perfil perpendiculares al 1 B y paralelos al 21B:

13

•      Se representan como cualquier recta de perfil con la peculiaridad de que sus trazas equidistan de LT y en el caso de la recta que está contenida en el 21 bisector, cualquier punto perteneciente a ella tiene igual cota que alejamiento.

Rectas de perfil perpendiculares al 21B y paralelas al 11B:

14

•      Se representan igual que otra recta de perfil, tienen sus trazas confundidas por encima, debajo o en LT dependiendo los cuadrantes que atraviesen.

Posiciones de rectas paralelas a la línea de tierra:

• Su representación, como ya hemos explicado, son dos líneas paralelas a LT, con características diferentes dependiendo de su posición con respecto a los planos de proyección.
•  
•  
•  
•  
•  
•  
•  

-------------------------------------------------------------------------------------------------------------------------

Diédrico: el Plano

DETERMINACIÓN DE UN PLANO

PERTENENCIAS

ALFABETO DEL PLANO